Quick start for `abess`: Linear regression

Brief introduction

The R package abess implement a polynomial algorithm for solving the best-subset selection problem: $\min_{\boldsymbol{\beta} \in \mathbb{R}^p} \mathcal{L_n}({\boldsymbol\beta}), \text{ s.t. } \|\boldsymbol\beta\|_0 \leq s,$ where $\mathcal{L}_{n}(\boldsymbol \beta)=\frac{1}{2 n}\|y-X \boldsymbol{\beta}\|_{2}^{2}$ , $\|\boldsymbol{\beta}\|_0=\sum_{i=1}^pI( \boldsymbol{\beta}_i\neq 0)$ is the $\ell_0$ (-pseudo) norm of $\beta$ , and the sparsity level $s$ is usually an unknown non-negative integer. Next, we present an example to show how to use the abess package to solve a simple problem.

Quick example

Fixed support size best subset selection

We generate a design matrix $X$ containing 300 observations and each observation has 1000 predictors. The response variable $y$ is linearly related to the first, second, and fifth predictors in $X$ : $y = 3X_1 + 1.5X_2 + 2X_5 + \epsilon,$ where $\varepsilon$ is a standard normal random variable.

library(abess)
synthetic_data <- generate.data(n = 300, p = 1000, 
                                beta = c(3, 1.5, 0, 0, 2, rep(0, 995)))
dim(synthetic_data[["x"]])

## [1]  300 1000

head(synthetic_data[["y"]])

##           [,1]
## [1,] -4.063922
## [2,]  3.855246
## [3,] -3.041391
## [4,] -1.081257
## [5,]  4.986772
## [6,]  4.470901

dat <- cbind.data.frame("y" = synthetic_data[["y"]], 
                        synthetic_data[["x"]])

Then, we use the main function abess in the package to fit this dataset. By setting the arguments support.size = s, abess() function conducts Algorithm 1 for the best-subset selection with a sparsity level s. In our example, we set the options: support.size = 3, and we run Algorithm 1 with the following command:

abess_fit <- abess(y ~ ., data = dat, support.size = 3)

The output of abess comprises the selected best model:

head(coef(abess_fit, sparse = FALSE))

##                       3
## (intercept) -0.01802179
## x1           2.96418205
## x2           1.45090693
## x3           0.00000000
## x4           0.00000000
## x5           1.90592036

The support set of the best model is identical to the ground truth, and the coefficient estimation is the same as the oracle estimator given by lm function:

lm(y ~ ., data = dat[, c(1, c(1, 2, 5) + 1)])

## 
## Call:
## lm(formula = y ~ ., data = dat[, c(1, c(1, 2, 5) + 1)])
## 
## Coefficients:
## (Intercept)           x1           x2           x5  
##    -0.01802      2.96418      1.45091      1.90592

Adaptive best subset selection

Supposing we are unknown about the true sparsity level in real world data, and thus, we need to determine the most proper one. The Algorithm 3 is designed for this scenario. abess is capable of performing this algorithm:

abess_fit <- abess(y ~ ., data = dat)

The output of abess() also comprises the selected best model:

best_size <- abess_fit[["best.size"]]
print(best_size)

## [1] 3

head(coef(abess_fit, support.size = best_size, sparse = FALSE))

##                       3
## (intercept) -0.01802179
## x1           2.96418205
## x2           1.45090693
## x3           0.00000000
## x4           0.00000000
## x5           1.90592036

The output model accurately detect the true model size, which implies the Algorithm 3 efficiently find both the optimal sparsity level and true effective predictors.

Real data example

Hitters Dataset

In this tutorial, we are going to demonstrate how to use the abess package to carry out best subset selection on the Hitters dataset. We hope to use several predictors related to the performance of the baseball athletes last year to predict their salary. First, let’s have a look at this dataset. There are 19 variables except Salary and 322 observations.

Hitters <- read.csv("Hitters.csv", header = TRUE)
head(Hitters)

##   AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks
## 1   293   66     1   30  29    14     1    293    66      1    30   29     14
## 2   315   81     7   24  38    39    14   3449   835     69   321  414    375
## 3   479  130    18   66  72    76     3   1624   457     63   224  266    263
## 4   496  141    20   65  78    37    11   5628  1575    225   828  838    354
## 5   321   87    10   39  42    30     2    396   101     12    48   46     33
## 6   594  169     4   74  51    35    11   4408  1133     19   501  336    194
##   League Division PutOuts Assists Errors Salary NewLeague
## 1      A        E     446      33     20     NA         A
## 2      N        W     632      43     10  475.0         N
## 3      A        W     880      82     14  480.0         A
## 4      N        E     200      11      3  500.0         N
## 5      N        E     805      40      4   91.5         N
## 6      A        W     282     421     25  750.0         A

dim(Hitters)

## [1] 322  20

sum(is.na(Hitters))

## [1] 59

Note that this dataset contains some missing data. So we use the na.omit() function to delete rows that have incomplete information. After that, we have 263 observations remaining.

Hitters <- na.omit(Hitters)
dim(Hitters)

## [1] 263  20

sum(is.na(Hitters))

## [1] 0

Then we change the factors into dummy variables with the model.matrix() function. Note that the abess() function will automatically include the intercept.

Hitters <- model.matrix(~., Hitters)[, -1]
Hitters <- as.data.frame(Hitters)

Running ABESS

The abess() function in the abess package allows you to perform best subset selection in a highly efficient way. You can call the abess() function using formula just like what you do with lm(). Or you can specify the design matrix x and the response y. The system.time() function records the run time.

library(abess)
abess_fit <- abess(Salary ~ ., Hitters)
abess_fit <- abess(Hitters[, -which(colnames(Hitters) == "Salary")], Hitters$Salary)
class(abess_fit)

## [1] "abess"

Interpret the Result

After get the estimator, we can further do more exploring work. The output of abess() function contains the best model for all the candidate support size in the support.size. You can use some generic function to quickly draw some information of those estimators.

# draw the estimated coefficients on all candidate support size
coef(abess_fit)

## 20 x 20 sparse Matrix of class "dgCMatrix"
##                                                                      
## (intercept) 535.9259 274.5803864 -47.9559022 -71.4592204   13.9231044
## AtBat         .        .           .           .            .        
## Hits          .        .           3.3008446   2.8038162    2.6757978
## HmRun         .        .           .           .            .        
## Runs          .        .           .           .            .        
## RBI           .        .           .           .            .        
## Walks         .        .           .           .            .        
## Years         .        .           .           .            .        
## CAtBat        .        .           .           .            .        
## CHits         .        .           .           .            .        
## CHmRun        .        .           .           .            .        
## CRuns         .        .           .           .            .        
## CRBI          .        0.7909536   0.6898994   0.6825275    0.6817790
## CWalks        .        .           .           .            .        
## LeagueN       .        .           .           .            .        
## DivisionW     .        .           .           .         -139.9538855
## PutOuts       .        .           .           0.2735814    0.2735002
## Assists       .        .           .           .            .        
## Errors        .        .           .           .            .        
## NewLeagueN    .        .           .           .            .        
##                                                                             
## (intercept)   -7.6563819   91.5117981   67.9431538  114.5067227  197.6616396
## AtBat          .           -1.8685892   -1.8535176   -2.1250564   -2.0803280
## Hits           2.0467293    7.6043976    7.6348879    7.6482495    6.8263359
## HmRun          .            .            .            .            .        
## Runs           .            .            .            .            .        
## RBI            .            .            .            .            .        
## Walks          2.5574106    3.6976468    3.6644212    5.2391412    5.9761215
## Years          .            .            .            .          -15.9414459
## CAtBat         .            .            .            .            .        
## CHits          .            .            .            .            .        
## CHmRun         .            .            .            .            .        
## CRuns          .            .            .            .            0.8143029
## CRBI           0.6492007    0.6430169    0.6445474    0.8959228    0.6000624
## CWalks         .            .            .           -0.3487728   -0.7503761
## LeagueN        .            .           35.0926551    .            .        
## DivisionW   -137.3676333 -122.9515338 -122.5437635 -126.8503150 -123.4936780
## PutOuts        0.2518721    0.2643076    0.2584749    0.2655057    0.2702288
## Assists        .            .            .            0.1790809    .        
## Errors         .            .            .            .            .        
## NewLeagueN     .            .            .            .            .        
##                                                                             
## (intercept)  206.5672285  218.5527334  198.4967427  142.9090129  144.6793182
## AtBat         -2.2556858   -2.2102483   -2.1783358   -2.0120568   -2.0883279
## Hits           7.0378766    6.9279436    6.9273744    7.3751935    7.6436454
## HmRun          .            .            .            .            2.3406524
## Runs           .            .            .           -1.7130320   -2.3580478
## RBI            .            .            .            .            .        
## Walks          6.2793246    6.2243570    6.1667822    5.9906173    6.1794713
## Years        -16.7414858  -17.2542087  -17.0664017    .            .        
## CAtBat         .            .            .           -0.1527096   -0.1488074
## CHits          .            .            .            .            .        
## CHmRun         .            .            .            .            .        
## CRuns          0.8132079    0.8111144    0.8082476    1.5535444    1.5931621
## CRBI           0.6508515    0.6594949    0.6571221    0.7850103    0.7170767
## CWalks        -0.7882990   -0.7934064   -0.7898841   -0.8404419   -0.8565844
## LeagueN        .            .           29.1474123   41.9165343   44.2352269
## DivisionW   -123.2261893 -123.1231837 -122.8009102 -112.3809790 -112.8079905
## PutOuts        0.2824819    0.2883338    0.2830813    0.2896964    0.2876182
## Assists        0.1872292    0.2795390    0.2732454    0.3312276    0.3677311
## Errors         .           -3.0198567   -3.3107203   -2.8685826   -3.1271251
## NewLeagueN     .            .            .            .            .        
##                                                                             
## (intercept)  163.3275824  163.0064063  162.9932027  163.1632541  163.1035878
## AtBat         -2.1085651   -2.0890552   -2.0302709   -2.0186239   -1.9798729
## Hits           7.6501026    7.8848050    7.7483580    7.7381465    7.5007675
## HmRun          2.3654025    3.8223369    4.6470956    4.6127592    4.3308829
## Runs          -2.3535049   -2.5377954   -2.5882384   -2.6272166   -2.3762100
## RBI            .           -0.8815425   -1.1165187   -1.1190038   -1.0449620
## Walks          6.1730276    6.2941910    6.2778803    6.3108843    6.2312863
## Years         -4.2321550   -4.0947594   -3.7490950   -3.8738277   -3.4890543
## CAtBat        -0.1341737   -0.1350897   -0.1526121   -0.1514014   -0.1713405
## CHits          .            .            .            .            0.1339910
## CHmRun         .            .           -0.3876922   -0.3938397   -0.1728611
## CRuns          1.5426322    1.5321626    1.5730263    1.5708067    1.4543049
## CRBI           0.7144063    0.7420886    0.8965235    0.8961782    0.8077088
## CWalks        -0.8446970   -0.8559654   -0.8423839   -0.8467366   -0.8115709
## LeagueN       42.2835360   42.2286763   41.6482699   61.3012822   62.5994230
## DivisionW   -113.9853363 -116.0422926 -116.4111439 -116.5862127 -116.8492456
## PutOuts        0.2859836    0.2858651    0.2827595    0.2829156    0.2818925
## Assists        0.3643305    0.3641325    0.3661464    0.3640952    0.3710692
## Errors        -3.2379385   -3.1409199   -3.1840695   -3.2558249   -3.3607605
## NewLeagueN     .            .            .          -22.9788245  -24.7623251

# get the deviance of the estimated model on all candidate support size
deviance(abess_fit)

##  [1] 101367.13  68782.66  58263.42  55607.03  53176.52  52241.95  49800.20
##  [8]  49651.96  49079.30  47327.31  47040.89  46947.37  46847.92  46177.09
## [15]  46100.11  46077.34  46053.29  46032.63  46016.41  46008.93

# print the fitted model
print(abess_fit)

## Call:
## abess.default(x = Hitters[, -which(colnames(Hitters) == "Salary")], 
##     y = Hitters$Salary)
## 
##    support.size       dev      GIC
## 1             0 101367.13 3031.471
## 2             1  68782.66 2934.538
## 3             2  58263.42 2895.944
## 4             3  55607.03 2888.729
## 5             4  53176.52 2882.033
## 6             5  52241.95 2882.427
## 7             6  49800.20 2874.896
## 8             7  49651.96 2879.170
## 9             8  49079.30 2881.177
## 10            9  47327.31 2876.675
## 11           10  47040.89 2880.136
## 12           11  46947.37 2884.671
## 13           12  46847.92 2889.171
## 14           13  46177.09 2890.436
## 15           14  46100.11 2895.055
## 16           15  46077.34 2899.983
## 17           16  46053.29 2904.903
## 18           17  46032.63 2909.843
## 19           18  46016.41 2914.808
## 20           19  46008.93 2919.824

Prediction is allowed for all the estimated models. Just call predict.abess() function with the support.size set to the size of model you are interested in. If support.size is not provided, prediction will be made on the model with best tuning value.

hitters_pred <- predict(abess_fit, 
                        newx = Hitters[, -which(colnames(Hitters) == "Salary")], 
                        support.size = c(3, 4))
head(hitters_pred)

##           3         4
## 2 611.11976  545.8175
## 3 715.34087  643.8563
## 4 950.55323 1017.2414
## 5 424.10211  498.2470
## 6 708.86493  632.3839
## 7  59.21692  139.8497

The plot.abess() function helps to visualize the change of models with the change of support size. There are 5 types of graph you can generate, including coef for the coefficient value, l2norm for the L2-norm of the coefficients, dev for the deviance and tune for the tuning value. Default if coef.

plot(abess_fit, label = TRUE)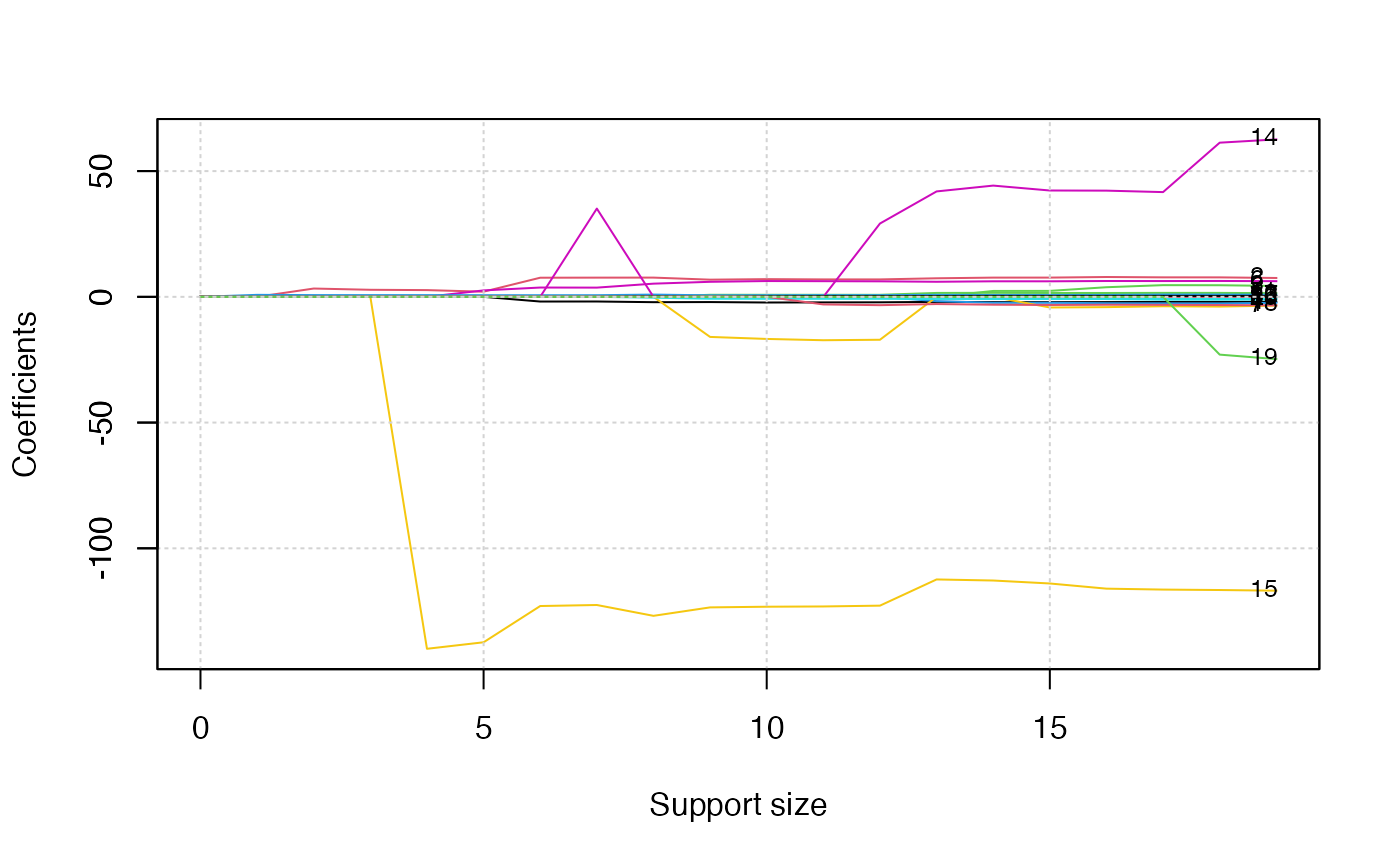

The graph shows that, beginning from the most dense model, the 15th variable (Division, A factor with levels E and W indicating player’s division at the end of 1986) is included in the active set until the support size reaches 3.

We can also generate a graph about the tuning value. Remember that we used the default GIC to tune the support size.

plot(abess_fit, type = "tune")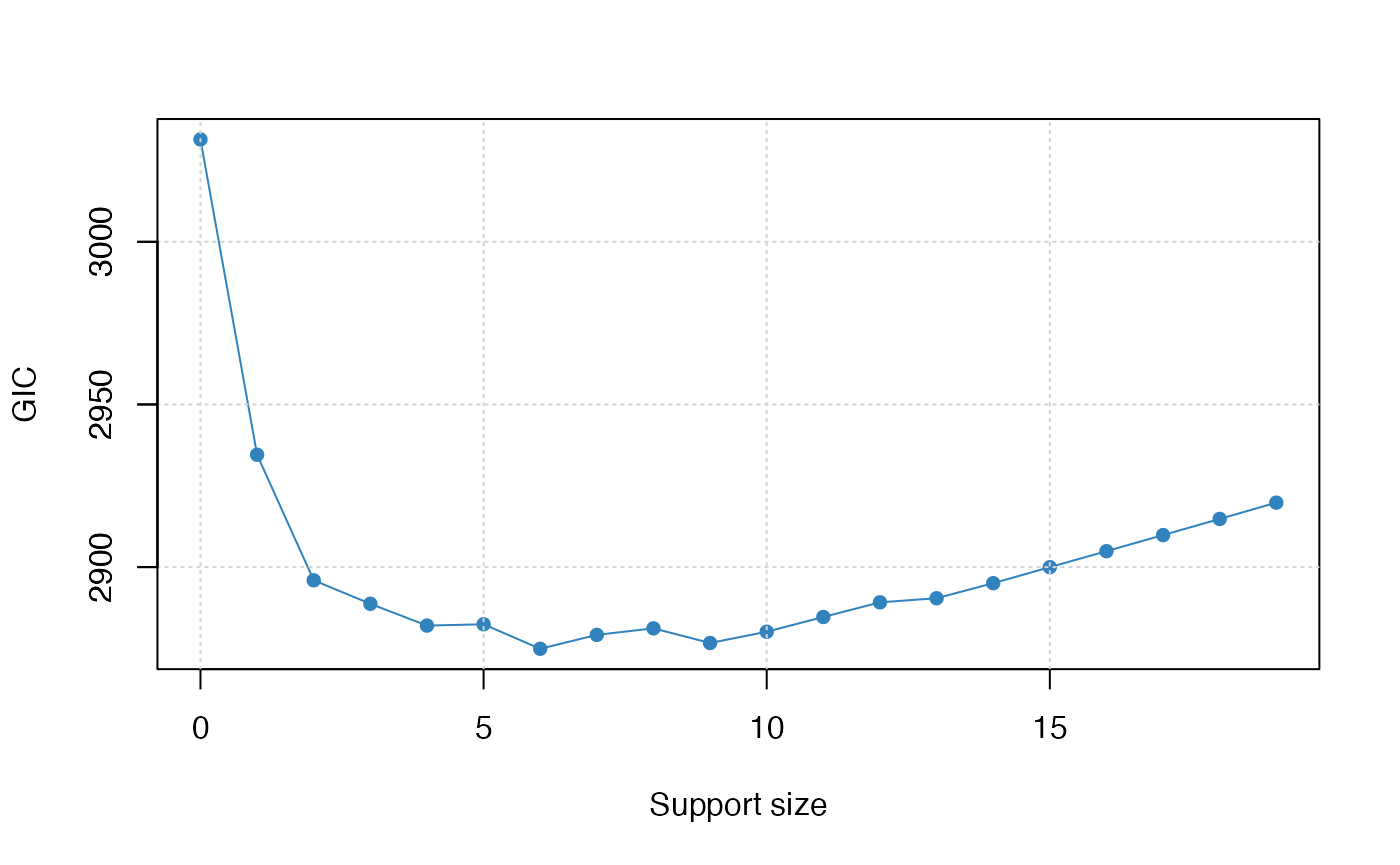

The tuning value reaches the lowest point at 6. And We might choose the estimated model with support size equals 6 as our final model. In fact, the tuning values of different model sizes are provided in tune.value of the abess object. You can get the best model size through the following call.

extract(abess_fit)[["support.size"]]

## [1] 6

To extract any model from the abess object, we can call the extract() function with a given support.size. If support.size is not provided, the model with the best tuning value will be returned. Here we extract the model with support size equals 6.

best.model <- extract(abess_fit, support.size = 6)
str(best.model)

## List of 7
##  $ beta        :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:6] 0 1 5 11 14 15
##   .. ..@ p       : int [1:2] 0 6
##   .. ..@ Dim     : int [1:2] 19 1
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:19] "AtBat" "Hits" "HmRun" "Runs" ...
##   .. .. ..$ : chr "6"
##   .. ..@ x       : num [1:6] -1.869 7.604 3.698 0.643 -122.952 ...
##   .. ..@ factors : list()
##  $ intercept   : num 91.5
##  $ support.size: num 6
##  $ support.vars: chr [1:6] "AtBat" "Hits" "Walks" "CRBI" ...
##  $ support.beta: num [1:6] -1.869 7.604 3.698 0.643 -122.952 ...
##  $ dev         : num 49800
##  $ tune.value  : num 2875

The return is a list containing the basic information of the estimated model.

Advanced features

Feature screening for ultra-high dimensional dataset

The consists of 18 variables about crime from the 1995 FBI UCR (e.g., per capita arson crimes and per capita violent crimes), communities information in the U.S. (e.g., the percent of the population considered urban), socio-economic data from the 90s census (e.g., the median family income), and law enforcement data from the 1990 law enforcement management and admin stats survey (e.g., per capita number of police officers). It would be appropriate if any of the crime state in community can be modeled by the basic community information, socio-economic and law enforcement state in community. Here, without the loss of generality, per capita violent crimes is chosen as the response variable, and 102 numerical variables as well as their pairwise interactions is considered as predictors. The pre-processed dataset for statistical modeling has 200 observations and 5253 predictors, and the code for pre-processing are openly shared in .
The pre-processed dataset can be freely downloaded by running:

working_directory <- getwd()
if (file.exists("crime.rda")) {
  load("crime.rda")
} else {
  crime_data_url <- "https://github.com/abess-team/abess/raw/master/R-package/data-raw/crime.rda"
  download.file(crime_data_url, "crime.rda")
  load(file.path(working_directory, "crime.rda"))
}

As mentioned before, this dataset comprises 5000+ features, much larger than the number of observations:

dim(crime)

## [1]  500 5254

And thus, it would be better to first perform feature screening, which is also supported by the abess function. Suppose we are interested in retaining 1000 variables with the largest marginal utility, then we can conduct the command:

abess_fit <- abess(y ~ ., data = crime, screening.num = 1000)
str(abess_fit)

## List of 14
##  $ beta          :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:528] 442 442 1196 374 442 1196 374 442 1003 1196 ...
##   .. ..@ p       : int [1:34] 0 0 1 3 6 10 15 21 28 36 ...
##   .. ..@ Dim     : int [1:2] 5253 33
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:5253] "pop" "perHoush" "pctBlack" "pctWhite" ...
##   .. .. ..$ : chr [1:33] "0" "1" "2" "3" ...
##   .. ..@ x       : num [1:528] -0.251 -0.196 0.496 0.812 -0.173 ...
##   .. ..@ factors : list()
##  $ intercept     : num [1:33] 599 2115 1668 1518 1189 ...
##  $ dev           : num [1:33] 190932 86423 80306 75780 72033 ...
##  $ tune.value    : num [1:33] 6080 5696 5672 5656 5643 ...
##  $ nobs          : int 500
##  $ nvars         : int 5253
##  $ family        : chr "gaussian"
##  $ tune.path     : chr "sequence"
##  $ tune.type     : chr "GIC"
##  $ support.size  : int [1:33] 0 1 2 3 4 5 6 7 8 9 ...
##  $ edf           : num [1:33] 0 1 2 3 4 5 6 7 8 9 ...
##  $ best.size     : int 8
##  $ screening.vars: chr [1:1000] "pctBlack" "pctWhite" "medIncome" "pctWdiv" ...
##  $ call          : language abess.formula(formula = y ~ ., data = crime, screening.num = 1000)
##  - attr(*, "class")= chr "abess"

The returned object of abess includes the features selected by screening. We exhibit six variables of them:

head(abess_fit[["screening.vars"]])

## [1] "pctBlack"     "pctWhite"     "medIncome"    "pctWdiv"      "pctPubAsst"  
## [6] "medFamIncome"

Then, by the generic extract function, we can obtain the best model detected by ABESS algorithm, and get the variables in the best model:

best_model <- extract(abess_fit)
str(best_model)

## List of 7
##  $ beta        :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:8] 303 374 1003 1196 1530 1746 2378 3266
##   .. ..@ p       : int [1:2] 0 8
##   .. ..@ Dim     : int [1:2] 5253 1
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:5253] "pop" "perHoush" "pctBlack" "pctWhite" ...
##   .. .. ..$ : chr "8"
##   .. ..@ x       : num [1:8] 0.192 1.071 1.867 0.301 -0.152 ...
##   .. ..@ factors : list()
##  $ intercept   : num -55.8
##  $ support.size: int 8
##  $ support.vars: chr [1:8] "pctBlack:pctWhite" "pctBlack:pctVacantBoarded" "pct65up:pctMaleDivorc" "pctUrban:pctKidsBornNevrMarr" ...
##  $ support.beta: num [1:8] 0.192 1.071 1.867 0.301 -0.152 ...
##  $ dev         : num 61304
##  $ tune.value  : num 5613

best_vars <- best_model[["support.vars"]]
best_vars

## [1] "pctBlack:pctWhite"             "pctBlack:pctVacantBoarded"    
## [3] "pct65up:pctMaleDivorc"         "pctUrban:pctKidsBornNevrMarr" 
## [5] "pctWdiv:pctEmployMfg"          "pctPubAsst:ownHousUperQ"      
## [7] "otherPerCap:pctHousWOphone"    "pctMaleDivorc:pctPopDenseHous"

More features

There are plenty features provided by abess packages such as logistic regression and group selection. Please the other articles in our website for more details.

Quick start for abess: Linear regression

Jin Zhu