Principal component analysis

Junhao Huang, Jin Zhu

Source: ../vignettes/v08-sPCA.Rmd 
Sys.setenv("OMP_THREAD_LIMIT" = 2)

Introduction

Principal component analysis (PCA) is an important method in the field of data science, which can reduce the dimension of data and simplify our model. It actually solve an optimization problem like:

\[ \max_{v} v^{\top}\Sigma v,\qquad s.t.\quad v^{\top}v=1. \]

where \(\Sigma = X^TX / (n-1)\) and \(X\) is the centered sample matrix. We also denote that \(X\) is a \(n\times p\) matrix, where each row is an observation and each column is a variable.

Then, before further analysis, we can project \(X\) to \(v\) (thus dimensional reduction), without losing too much information.

However, consider that:

  • The PC is a linear combination of all primary variables (\(Xv\)), but sometimes we may tend to use less variables for clearer interpretation (and less computational complexity);

  • It has been proved that if \(p/n\) does not converge to \(0\), the classical PCA is not consistent, but this would happen in some high-dimensional data analysis.

For example, in gene analysis, the dataset may contain plenty of genes (variables) and we would like to find a subset of them, which can explain most information. Compared with using all genes, this small subset may perform better on interpretation, without loss much information. Then we can focus on these variables in the further analysis.

When we are trapped by these problems, a classical PCA may not be a best choice, since it use all variables. One of the alternatives is abessPCA, which is able to seek for principal component with a sparsity limitation:

\[ \max_{v} v^{\top}\Sigma v,\qquad s.t.\quad v^{\top}v=1,\ ||v||_0\leq s. \]

where \(s\) is a non-negative integer, which indicates how many primary variables are used in principal component. With abessPCA, we can search for the best subset of variables to form principal component and it retains consistency even under \(p>>n\). And we make two remarks:

  • Clearly, if \(s\) is equal or larger than the number of primary variables, this sparsity limitation is actually useless, so the problem is equivalent to a classical PCA.
  • With less variables, the PC must have lower explained variance. However, this decrease is slight if we choose a good \(s\) and at this price, we can interpret the PC much better. It is worthy.

In the next section, we will show how to form abessPCA in our frame.

abessPCA: real data example

Communities-and-crime dataset

Here we will use real data analysis to show how to form abessPCA. The data we use is from UCI: Communities and Crime Data Set.

X <- read.csv('./communities.data', header = FALSE, na.strings = '?')
dim(X)
## [1] 1994  128

The dataset contain 128 variables but a part of them have missing values or categorical variables. We simply drop these variables, and retain 99 predictive variables as our data example.

X <- X[, 6:127]
na_col <- apply(X, 2, anyNA)
X <- X[, !na_col]
dim(X)
## [1] 1994   99

Adaptive best subset selection for PCA

Next, we turn to fit abessPCA. For fitting the model, we can give either predictor matrix \(X\):

## 
##  Thank you for using abess! To acknowledge our work, please cite the package:
## 
##  Zhu J, Wang X, Hu L, Huang J, Jiang K, Zhang Y, Lin S, Zhu J (2022). 'abess: A Fast Best Subset Selection Library in Python and R.' Journal of Machine Learning Research, 23(202), 1-7. https://www.jmlr.org/papers/v23/21-1060.html.
best_pca <- abesspca(X)
str(best_pca)
## List of 15
##  $ coef        :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:4950] 70 10 70 11 76 83 11 76 81 83 ...
##   .. ..@ p       : int [1:100] 0 1 3 6 10 15 21 28 36 45 ...
##   .. ..@ Dim     : int [1:2] 99 99
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:99] "V6" "V7" "V8" "V9" ...
##   .. .. ..$ : chr [1:99] "1" "2" "3" "4" ...
##   .. ..@ x       : num [1:4950] 1 -0.641 -0.767 -0.899 0.31 ...
##   .. ..@ factors : list()
##  $ tune.value  : num [1:99] 0 0 0 0 0 0 0 0 0 0 ...
##  $ ev          : num [1:99, 1] 0.0226 0.0369 0.228 0.2487 0.2736 ...
##  $ kpc.num     : num 1
##  $ var.pc      : num [1:99] 1.065 0.752 0.33 0.284 0.184 ...
##  $ cum.var.pc  : num [1:99] 1.07 1.82 2.15 2.43 2.62 ...
##  $ var.all     : num 3.97
##  $ pev         : num [1:99, 1] 0.00571 0.00931 0.05748 0.0627 0.06898 ...
##  $ pev.pc      : num [1:99, 1] 0.0212 0.0347 0.214 0.2335 0.2568 ...
##  $ nvars       : int 99
##  $ sparse.type : chr "fpc"
##  $ support.size: num [1:99] 1 2 3 4 5 6 7 8 9 10 ...
##  $ tune.type   : chr "gic"
##  $ tune.path   : chr "sequence"
##  $ call        : language abesspca(x = X)
##  - attr(*, "class")= chr "abesspca"

or Gram-type matrix (like covariance matrix, correlation matrix and robust covariance matrix):

best_pca <- abesspca(cov(X), type = "gram")
str(best_pca)
## List of 15
##  $ coef        :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:4950] 70 10 70 11 76 83 11 76 81 83 ...
##   .. ..@ p       : int [1:100] 0 1 3 6 10 15 21 28 36 45 ...
##   .. ..@ Dim     : int [1:2] 99 99
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:99] "V6" "V7" "V8" "V9" ...
##   .. .. ..$ : chr [1:99] "1" "2" "3" "4" ...
##   .. ..@ x       : num [1:4950] 1 -0.641 -0.767 -0.899 0.31 ...
##   .. ..@ factors : list()
##  $ tune.value  : num [1:99] 0 0 0 0 0 0 0 0 0 0 ...
##  $ ev          : num [1:99, 1] 0.0226 0.037 0.2281 0.2488 0.2739 ...
##  $ kpc.num     : num 1
##  $ var.pc      : num [1:99] 1.066 0.752 0.33 0.284 0.185 ...
##  $ cum.var.pc  : num [1:99] 1.07 1.82 2.15 2.43 2.62 ...
##  $ var.all     : num 3.97
##  $ pev         : num [1:99, 1] 0.00571 0.00931 0.05748 0.0627 0.06901 ...
##  $ pev.pc      : num [1:99, 1] 0.0212 0.0347 0.214 0.2335 0.257 ...
##  $ nvars       : int 99
##  $ sparse.type : chr "fpc"
##  $ support.size: num [1:99] 1 2 3 4 5 6 7 8 9 10 ...
##  $ tune.type   : chr "gic"
##  $ tune.path   : chr "sequence"
##  $ call        : language abesspca(x = cov(X), type = "gram")
##  - attr(*, "class")= chr "abesspca"

Interpreting result

After fitting abessPCA, we study the percentage of explained variance as \(s\) increases:

plot(best_pca[["support.size"]], best_pca[["pev"]], type = "l")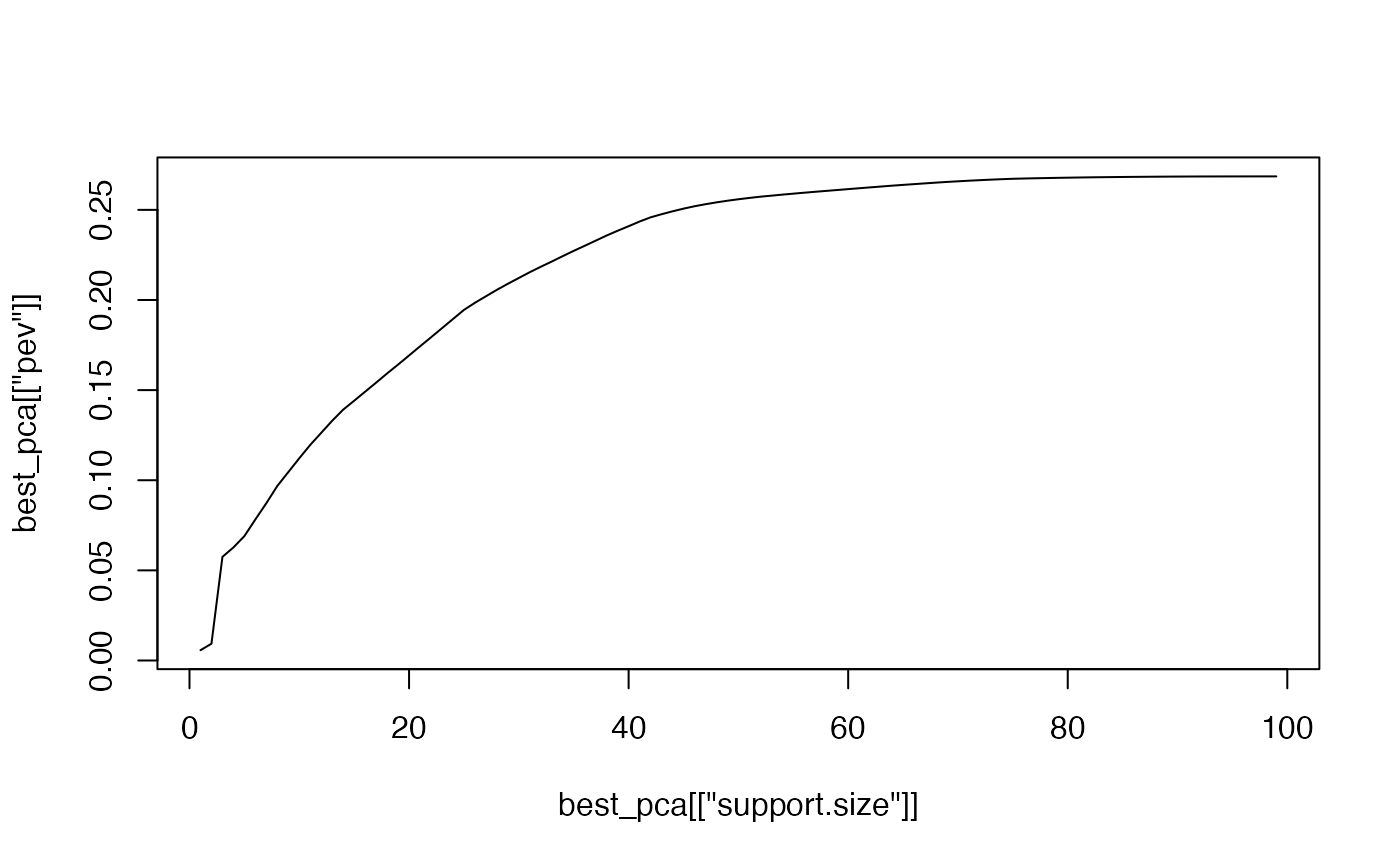

It is clear that the higher sparsity is, the more variance it can explain. Interestingly, we can seek for a smaller sparsity which can explain most of the variance. For instance, when 40 variables are selected, the percentage of explained variance from abessPCA exceeds 80%.
This result shows that using less than half of all 99 variables can be close to perfect. We can use coef function to investigate which variables are selected when the explained variance are large. For example, if we choose sparsity 40, the used variables are:

coef(best_pca, support.size = 40)
## 99 x 1 sparse Matrix of class "dgCMatrix"
##              40
## V6    .        
## V7    .        
## V8   -0.1365515
## V9    0.1227176
## V10   .        
## V11   .        
## V12   .        
## V13   .        
## V14   .        
## V15   .        
## V16   .        
## V17   0.1745626
## V18   0.1999679
## V19   0.1117617
## V20   .        
## V21   0.1559536
## V22   .        
## V23  -0.1808407
## V24   .        
## V25   0.1912228
## V26   0.1715435
## V27   0.1505258
## V28   0.1140740
## V29   .        
## V30   .        
## V32   0.1174763
## V33   .        
## V34  -0.1981478
## V35  -0.1561935
## V36  -0.1673926
## V37   0.1551137
## V38  -0.1588460
## V39   0.1167834
## V40   .        
## V41   .        
## V42  -0.1451945
## V43   0.1448450
## V44  -0.1137527
## V45   .        
## V46  -0.1069923
## V47  -0.1164267
## V48   .        
## V49   0.1697180
## V50   0.1756634
## V51   0.1881001
## V52   0.1389346
## V53   .        
## V54   .        
## V55   .        
## V56  -0.1542476
## V57   .        
## V58   .        
## V59   .        
## V60   .        
## V61   .        
## V62   .        
## V63   .        
## V64   .        
## V65   .        
## V66   .        
## V67   .        
## V68   .        
## V69   .        
## V70   .        
## V71   .        
## V72   .        
## V73   0.1208047
## V74   .        
## V75   .        
## V76   0.1056635
## V77   .        
## V78   .        
## V79   .        
## V80  -0.1118632
## V81   .        
## V82   .        
## V83  -0.2118385
## V84  -0.1127914
## V85   0.1789415
## V86   0.1819897
## V87   0.1818463
## V88   0.1831991
## V89   0.1793673
## V90   0.2122642
## V91   0.1823010
## V92   .        
## V93   .        
## V94   .        
## V95   .        
## V96   .        
## V97   .        
## V98   .        
## V99   .        
## V100  .        
## V101  .        
## V119  .        
## V120  .        
## V121  .        
## V126  .

where each row of loading matrix corresponds to a variable.

Extension

Group variable

In some cases, some variables may need to consider together, that is, they should be “used” or “unused” for PC at the same time, which we call “group information”. The optimization problem becomes:

\[ \max_{v} v^{\top}\Sigma v,\qquad s.t.\quad v^{\top}v=1,\ \sum_{g=1}^G I(||v_g||\neq 0)\leq s. \]

where we suppose there are \(G\) groups, and the \(g\)-th one correspond to \(v_g\), \(v = [v_1^T,v_2^T,\cdots,v_G^T]^T\). Then we are interested to find \(s\) (or less) important groups.

Group problem is extraordinary important in real data analysis. Still take gene analysis as an example, several sites would be related to one pathway, and it is meaningless to consider each of them alone.

abessPCA can also deal with group information. Here we make sure that variables in the same group address close to each other (if not, the data should be sorted first).

Suppose that the data above have group information like:

  • Group 1: {the 1st, 2nd, …, 6th variable};
  • Group 2: {the 7th, 8th, …, 12th variable};
  • …
  • Group 16: {the 91st, 92nd, …, 96th variable};
  • Group 17: {the 97th, 98th, 99th variables}.

Denote different groups as different number:

g_info <- c(rep(1:16, each = 6), rep(17, 3))

And fit a group SPCA model with additional argument group.index = g_info:

best_pca <- abesspca(X, group.index = g_info)
str(best_pca)
## List of 15
##  $ coef        :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. ..@ i       : int [1:912] 42 43 44 45 46 47 18 19 20 21 ...
##   .. ..@ p       : int [1:18] 0 6 18 36 60 90 126 168 216 270 ...
##   .. ..@ Dim     : int [1:2] 99 17
##   .. ..@ Dimnames:List of 2
##   .. .. ..$ : chr [1:99] "V6" "V7" "V8" "V9" ...
##   .. .. ..$ : chr [1:17] "1" "2" "3" "4" ...
##   .. ..@ x       : num [1:912] -0.503 -0.512 -0.5279 -0.4516 0.0472 ...
##   .. ..@ factors : list()
##  $ tune.value  : num [1:17] 0 0 0 0 0 0 0 0 0 0 ...
##  $ ev          : num [1:17, 1] 0.158 0.388 0.471 0.561 0.645 ...
##  $ kpc.num     : num 1
##  $ var.pc      : num [1:99] 1.065 0.752 0.33 0.284 0.184 ...
##  $ cum.var.pc  : num [1:99] 1.07 1.82 2.15 2.43 2.62 ...
##  $ var.all     : num 3.97
##  $ pev         : num [1:17, 1] 0.0399 0.0979 0.1188 0.1415 0.1625 ...
##  $ pev.pc      : num [1:17, 1] 0.148 0.364 0.442 0.527 0.605 ...
##  $ nvars       : int 99
##  $ sparse.type : chr "fpc"
##  $ support.size: num [1:17] 1 2 3 4 5 6 7 8 9 10 ...
##  $ tune.type   : chr "gic"
##  $ tune.path   : chr "sequence"
##  $ call        : language abesspca(x = X, group.index = g_info)
##  - attr(*, "class")= chr "abesspca"

Multiple principal components

In some cases, we may seek for more than one principal components under sparsity. Actually, we can iteratively solve the largest principal component and then mapping the covariance matrix to its orthogonal space:

\[ \Sigma' = (1-vv^{\top})\Sigma(1-vv^{\top}) \]

where \(\Sigma\) is the covariance matrix and \(v\) is its (sparse) loading vector. We map it into \(\Sigma'\), which indicates the orthogonal space of \(v\), and then solve the sparse principal component for \(\Sigma'\) again. By this iteration process, we can acquire multiple principal components and they are sorted from the largest to the smallest. In our program, there is an additional argument sparse.type to support this feature. By setting sparse.type = "kpc", then best subset selection performs on the first \(K\) principal components where \(K\) is decided by argument support.size.

Suppose we are interested in the first two principal components, and the support size is 50 in the first loading vector and is 40 in the second loading vector. In other words, we consecutively solve two problem: \[ v_1 \leftarrow \arg\max_{v} v^{\top}\Sigma v,\qquad s.t.\quad v^{\top}v=1,\ ||v||_0\leq 10, \] \[ v_2 \leftarrow \arg\max_{v} v^{\top} \Sigma^{\prime} v,\qquad s.t.\quad v^{\top}v=1,\ ||v||_0\leq 5, \] where \(\Sigma^{\prime} = (1-v_1 v_1^\top)\Sigma(1-v_1 v_1^\top)\). The \((v_1, v_2)\) forms a sparse loading matrix.

The code for solving the two problem is:

best_kpca <- abesspca(X, support.size = c(50, 40), sparse.type = "kpc")
str(best_kpca)
## List of 15
##  $ coef        :List of 2
##   ..$ :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. .. ..@ i       : int [1:90] 2 3 11 12 13 15 17 19 20 21 ...
##   .. .. ..@ p       : int [1:3] 0 40 90
##   .. .. ..@ Dim     : int [1:2] 99 2
##   .. .. ..@ Dimnames:List of 2
##   .. .. .. ..$ : chr [1:99] "V6" "V7" "V8" "V9" ...
##   .. .. .. ..$ : chr [1:2] "40" "50"
##   .. .. ..@ x       : num [1:90] -0.136 0.123 0.175 0.2 0.111 ...
##   .. .. ..@ factors : list()
##   ..$ :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   .. .. ..@ i       : int [1:90] 1 3 4 5 11 17 38 41 49 51 ...
##   .. .. ..@ p       : int [1:3] 0 40 90
##   .. .. ..@ Dim     : int [1:2] 99 2
##   .. .. ..@ Dimnames:List of 2
##   .. .. .. ..$ : chr [1:99] "V6" "V7" "V8" "V9" ...
##   .. .. .. ..$ : chr [1:2] "40" "50"
##   .. .. ..@ x       : num [1:90] 0.071 -0.171 0.159 0.211 0.171 ...
##   .. .. ..@ factors : list()
##  $ ev          :List of 2
##   ..$ : num [1:2, 1] 0.955 1.015
##   ..$ : num [1:2] 1.75 1.77
##  $ tune.value  :List of 2
##   ..$ : num [1:2, 1] 371 464
##   ..$ : num [1:2, 1] 371 464
##  $ kpc.num     : num 2
##  $ var.pc      : num [1:99] 1.065 0.752 0.33 0.284 0.184 ...
##  $ cum.var.pc  : num [1:99] 1.07 1.82 2.15 2.43 2.62 ...
##  $ var.all     : num 3.97
##  $ pev         :List of 2
##   ..$ : num [1:2, 1] 0.241 0.256
##   ..$ : num [1:2] 0.441 0.446
##  $ pev.pc      :List of 2
##   ..$ : num [1:2, 1] 0.897 0.953
##   ..$ : num [1:2] 0.962 0.972
##  $ nvars       : int 99
##  $ sparse.type : chr "kpc"
##  $ support.size:List of 2
##   ..$ : num [1:2] 40 50
##   ..$ : num [1:2] 40 50
##  $ tune.type   : chr "gic"
##  $ tune.path   : chr "sequence"
##  $ call        : language abesspca(x = X, sparse.type = "kpc", support.size = c(50, 40))
##  - attr(*, "class")= chr "abesspca"

The result best_kpca[["pev"]] shows that two principal components raised from two loading matrix could explain 40% variance of all variables (i.e., \(\text{trace}(\Sigma)\)).